Musicology and mathematics

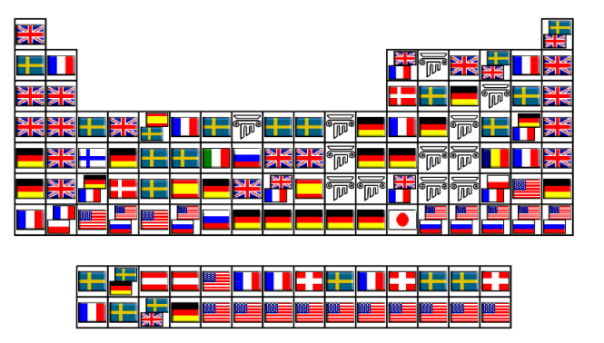
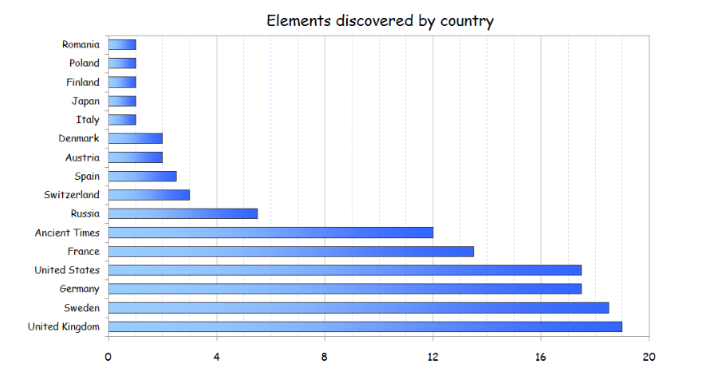
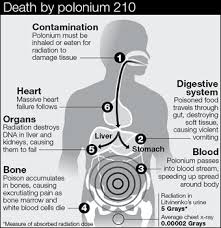
Among multiple possibilities that contain mathematics, mathematical intercourses allow to synthesise  scale’s notes in order to ensure a perfect harmony.

One interesting application is the canon written by JS Bach of his “musical offering”.

He combined the notes in the good place, upside, and criss-crossed and superposed.

It called the notion of a Moebius band. It’s a geometric figure with very interesting properties:

It’s a 3D geometric figure which has only one face and can’t be cut in two its length :

Leibnitz quoting ” music is an exercise in arithmetic as mind ignores that there are”

Effectively, all notes are 3/2 multiples, it’s the circle of fifths.

We can find

• the cycle of ascending fifths
• the cycle of descending fifths
• and alternating circle of fifths

Therefore, when we talk about range we’d rather talk about spiral of fifths:

 

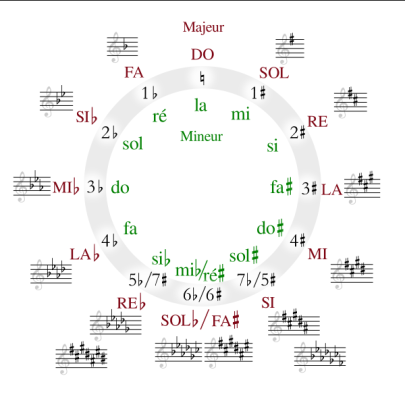On the right of every note we find the note that is a straight above.

According to a tense rope,  mathematicians like Pythagorus have noticed when we devised  into two the length of the rope we obtain the same note but a two times acuter  musical sound. (In fact we multiply the frequency of the initial sound by two. It is said that the sound is an octave higher. While when  dividing the frequency of a sound by 3/2 it gives a different sound, acuter. It is said that the sound is a higher straight.

Thus, all the musical range is built on 3/2 multiples

 

Swern oxidation mechanism

Swern oxidation mechanism is useful to convert terminal alcohol into aldehyde or ketone.

You need to work using (COCl)2, DMSO and triethylamine base.

Nice publication about cristal growing

Some thoughts about the single crystal growth of small molecules†

Bernhard Spingler,* Stephan Schnidrig, Tonya Todorova and Ferdinand Wild

DOI: 10.1039/c1ce05624g

This highlight critically compares various techniques to grow single crystals when only a few milligrams are available of the compound of interest. The authors describe vapour diffusion, evaporation, cooling, and layering techniques, as well as crystallisation in gels. A table of successfully applied solvent/antisolvent combinations for initial screening is given. Additionally, a comprehensive table of 107 solvents with their boiling points, densities and dielectric constants helps to optimise the crystal growth.

find number 6 !!

Only using mathematical signs ( + –  division square roots, ….) find for the numbers until 9 , the combinaison which gives 6 (answers in red)

 

1  1  1  = 6

2 2 2 = 6

3 3 3 = 6

4 4 4 = 6

5 5 5 =6

6 6 6= 6

7 7 7 =6

8 8 8 = 6

9 9 9 = 6

The Mask

The mask, this is what you put on your face for a better life, with it you are happy.

Everybody thinks because each one has a mask.

We live in a mask’s world.

Stay where you are, stored in your box.

otherwise people watch you, badly.

The eyes of others is important.

But, a mask is never eternal.

Sometimes it falls and you are hurt.

 

A guide to interprete mass spectra

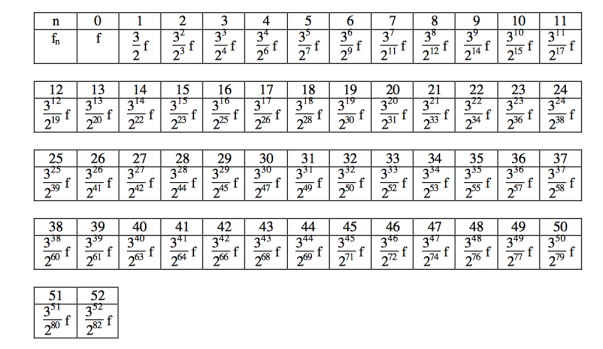
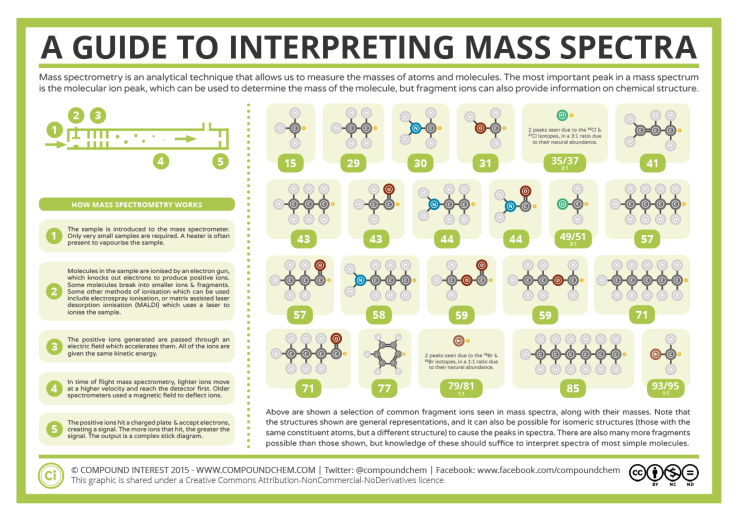So according to this table you can deduce a mass of 15 u.a is a fragment CH3:

M(C)=12 g/mol

M(H)=1 g/mol

and CH3 is 12 + 3 x 1 = 15

Periodic table, an international work

As you can see The Periodic Table is completely international !

Romans and Greeks described twelve elements.

Scientists of 15 different countries have discovered the remaining 106 elements.

19 elements of those have been co-discovered by researchers of two countries.

Although some of them such as Bromine, Thallium were isolated by chemists of different nationalities.

Collaborative researches have also led to discover recently four new elements whose: Ununpentium, Ununseptium and Ununoctium.

Polish Maria Skodowska-Curie and her French husband, Pierre Curie, effected isolation of Radium and Polonium.

 

 

It’s wonderful to see Periodic Table, something we use everyday in chemistry field, is in fact the result of a collective and very long-term work of international scientists.

 

Reference: Article of Enrique Domínguez Álvarez

Radical reactions

Radical reactions can be initiated by light or by the presence of peroxides . These reactions are not sensible with the solvent polarity.

There are always three steps in radical reactions. A radical reaction involves the formation of a carbonyl radical. The radicals are formed by homolytic cleavage of a bond:

First step: boot

During this first step, there is the formation of an initiator radical which allows the following steps to occur. This radical comes from the homolytic cleavage of a bond. This operation needs an energy called “activation energy” and could provides:

• by the warmth (we give a kinetic energy to the molecules)
• or by photons hv: it’s a photochemical reaction.

• or by chemical way: the peroxides promote the formation of the radicals, it’s a thermochemical initiation.

Second step: propagation

This step occurs, generally, into two steps: the initiator radical previously formed reacts on the carbon substrate and leads to the formation of a new carbon radical. During this second step of propagation, the carbon radical reacts with a new reagent molecule.

Third step: termination or cessation

The radicals and the free atoms able to perform covalent bonds directly between them. The propagation of the chains generating radicals or atoms stops.

The most poisonous substances

The most poisonous substances often gathered based on their acute toxicity as measured by LD50: Lethal Dose.

LD50 is a mesure of the dose in a substance which kill half of a given population.

Here are presented the five most poisonous substances:

1. Botulinum toxins

Botulinum toxins are included in the family of neurotoxins and contains the most toxic substance known on human.

2. Snake venom

Most snake venom are a mixture of several proteins which are often neurotoxins. The speed of activity makes that some venoms might kill very quickly. This is a crucial information because a potent but slow-acting venom can leave enough to intervenes whereas a fast-acting poison with a lower LD50 can kill in some seconds.

3. Arsenic

Arsenic is a very toxic metals. This metal decouples the respiratory chain by substitution with phosphorus.

4. Polonium-210

Polonium kills by emitting radiation which shreds sensitive biomolecule such as DNA and kills cells. The death is slow because of radiation poisoning.

5. Mercury

Mercury is a type of metal poisoning. This is a heavy metal occurring in several forms. Less than one gram of this metal produce high toxicity or death. Mercury acts by blocking blood vessels.

 

 

Very good chemistry QCM

This QCM is about several concepts in chemistry , you can see very easy QCM but some QCM where you need some knowledges or reflection.

Test your memory or you level in chemistry by this way!

http://www.ucl.ac.uk/clie/placement-tests/UPC/complete.php?exercise=Chemistry

Good luck, hope 30/30 !!